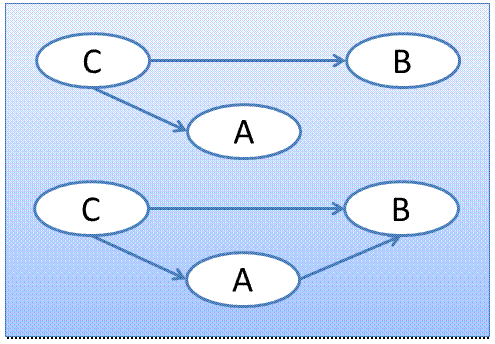
擬似相関についての補足
イノベーション方法論第1回,おつかれさまでした。
昨日講義後にお話ししていてうまく説明できていなかった部分をいくつか補足します。
A→Bを元々主張していたら,真の原因変数Cによって生じている擬似相関でないかとコメントを受けた,という状況を想定します。
Q1 A→Bの因果を擁護するためには,どのような方法があるのか(佐々木さん)
Q2 A→Bの因果が消えるかどうかはどうやって判定するのか(高田さん)
どちらの疑問点もC→A,C→Bというモデルなのか(擬似相関であり,A→Bの因果は存在しない),C→A→B,C→B(Cが真の原因変数だけれども,A→Bの因果も確かに存在する)なのかという部分に関連する問いだったと理解しています。
自然言語(文章とか事例記述)の場合はA→Bの説得力の問題となります。
昨日お話ししたA→B擁護の仕方は,A→D→Bとなるような,A→Bの間に関する記述を増やすとか,CとDとは関係がないことを主張する,という方法でした。
そのほかにもA→Cの逆因果を検討する方法もあるかもしれません(Cが真の原因変数,というほどではなくなる)。この場合は,Bに対してAもCも原因としてありそうだね,ということになります。
統計手法を利用する場合には,もう少し明確で,構造方程式モデリングとかパス解析(重回帰分析と因子分析の組み合わせ応用編のようなものです)を利用すると,昨日の授業であつかったようなノモロジカル・ネットの図そのままに統計分析をすることができます。この場合は,Cを原因変数としてモデルに組み込んだ場合に,A→Bの因果パスが消えるか,あるいはどの程度弱まるか,等が数値で示されるのでわりと明快だとおもいます。